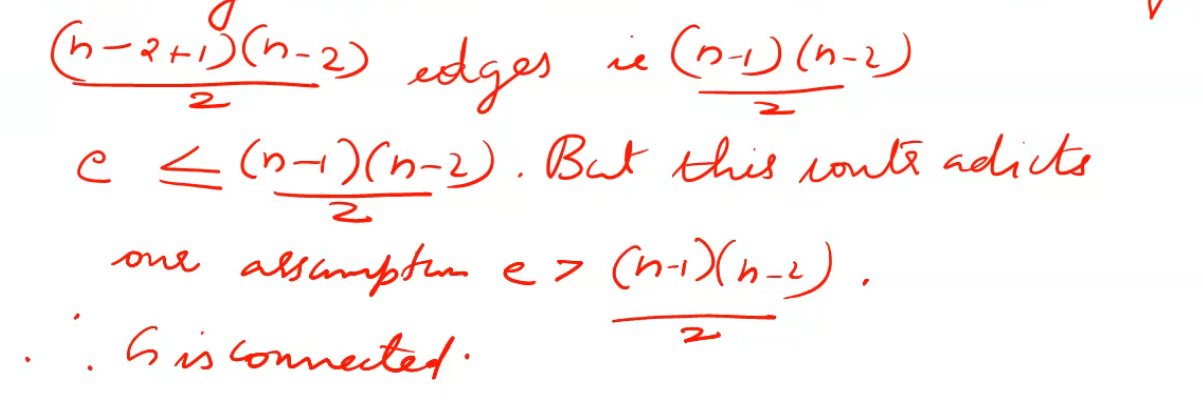quest:

What is the largest number of vertices in a graph with 35 edges and if all vertices have degree atleast 3?

ans:

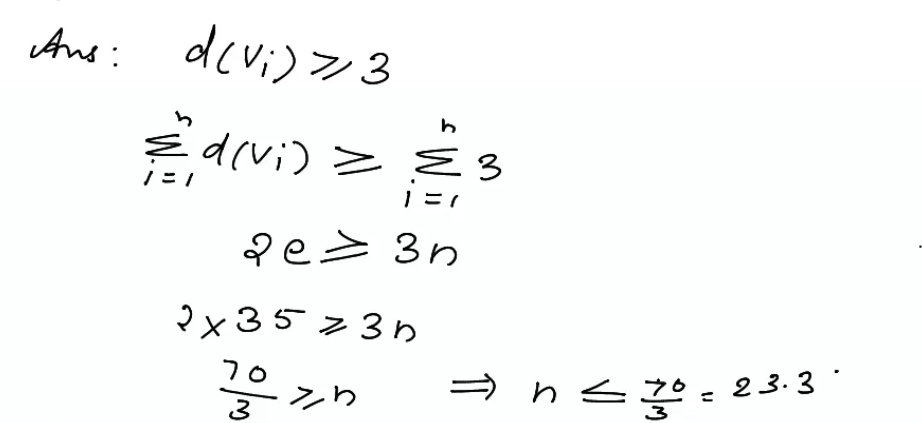Max no of vertices = 23

Theorem:

a simple graph with n vertices and k components can have at most (n-k)(n-k+1)/2 edges

Proof

Let the number of vertices in each of the k components of a graph G be n1,n2,…,nk.

Thus n1+n2+…+nk = n, n i>=1

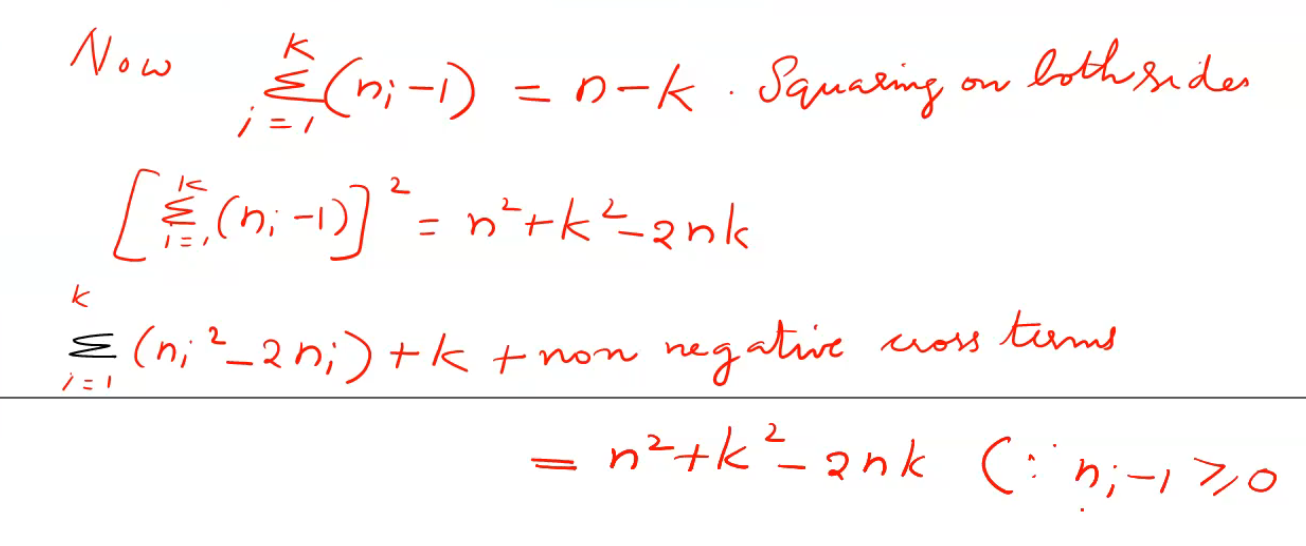
Now the max number of edges in the i the componenet of G is ni(ni-1)/2 . Therefore the max no of edges in G is

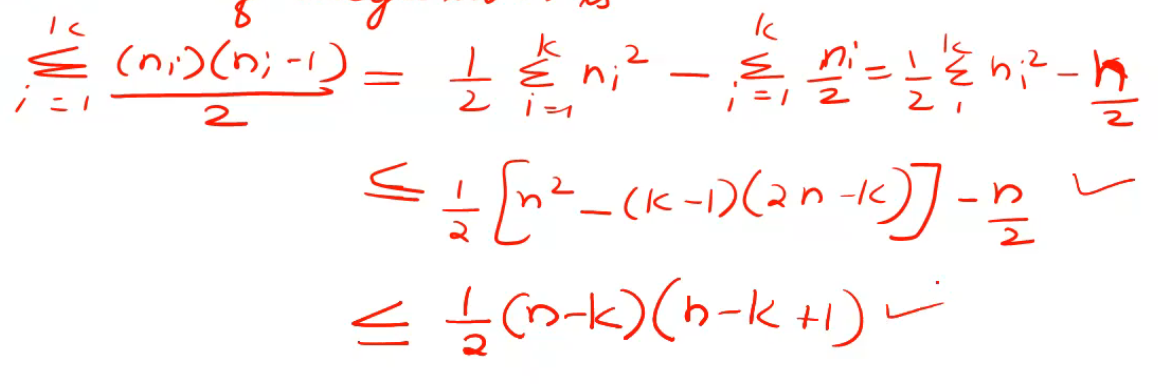
Prove that

a simple graph with n vertices is connnected if it has more than (n-1)(n-2)/2

ans:

Suppose G has more than (n-1)(n-2)/2 edges and is diconnected say with 2 componets . Then by above theorem it has maximum of (n-2+1)(n-2)/2edges