examples of a non isomorphic graph

![isomorphicandNonIsomorphicGraphs][./img/isomorphicandNonIsomorphicGraphs.png]

Two isomorphic graphs must have

1. the same number of vertices
2. the same number of edges
3. an equal number of vertices with a given degre.
4. Same degree sequence.

These conditions are not sufficient

There are non-isomorphic graphs which satisfy all these conditions.

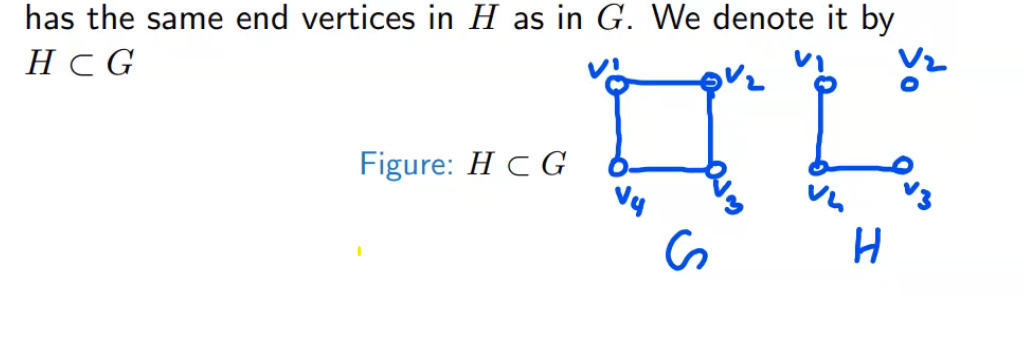
A graph H is said to be a subgraph of a graph G if all the vertices and all the edges of H are in G, and each edge of H has the same end vertices in H as in G. We denote it by

An open walk in which no vertex appears more than once is called its path.

• the number of edges in a path is called the length of a path

• A self-loop can be included in a walk but not in a path

• The terminal vertices of a path are of degree one, and the rest of the vertices (called the intermediate vertices) are of degree two.

• A closed walk in which no vertex(excep the start and end) appears more than once is called a circuit. It is closed

  nonintersecting walk.

• Every vertex in a circuit is of degree two.

• A circuit is also called a cycle, elementary cycle, circular path and polygon.