Mod2- Eulerian and Hamiltonian Graph

Euler graphs
Operations o n graphs
Hamiltonian path + circuits
Travelling Salesman problem
Directed graphs- types of digraphs
Digraphs & Binary relation
Directed paths
Fleurey’s algorithm

Operations on Graphs

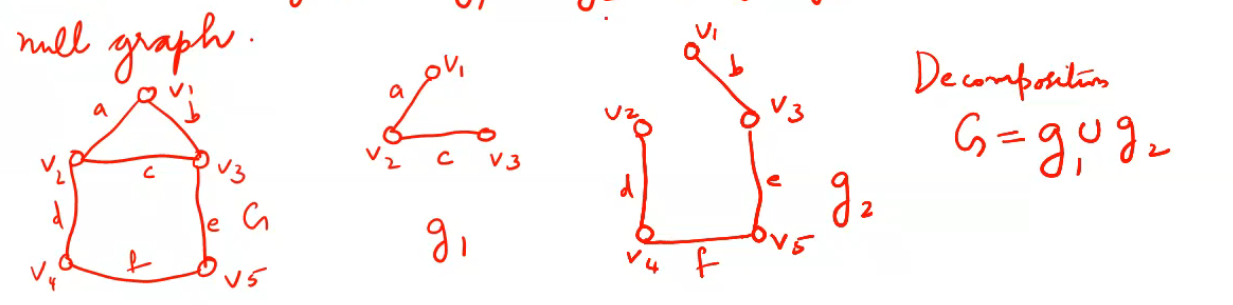
The union of graphs G1=(V1,E1) and G2=(V2,E2) is another graph G3 (Written as G3=G1UG2 whose vertex set V3=V1UV2 and the edge seett E3=E1UE2

Mod2G1UG2

Intersection

The Intersection G1UG2 of graphs G1 and G2 is a graph G4 consisting only og those vertices and edges that are in both G1 and G2

Ring Sum

The Ring Sum of two graphs G1 and G2 (written as G1 +O+(Xor symbol) G2) is a graph consisting of vertex set V1Uv2 and of edges that are either in G1 or G2 but not in both

RingSum

If g is asubgraph of G, then G(xor symbol)g is, by definition,that subgraph of G which remains after all the edges in g haave been removed from G. Therefore G(xor)g is written as G-g whenever g<=G. Because fo this complemetary nature, G(xor)g=G-g is often called the complement of g in G.

The complement of a graph G is definved as G’=Kn-G

A graph which is isomorphic to its complement is called self complementary graph.

$complementaryGraphEg$

Decomposition: A graph G is said to have been decomposed into two subgraphs g1, and g2 if g1 U g2 =G and G1 intersection g2 is a null graph.

$decompositiongraph$

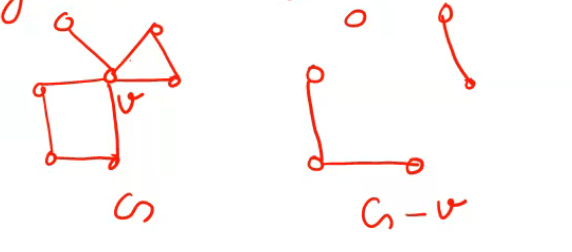
Vertex deleted Subgraph

If vi is a vertex in a graph G, then G-vi denotes the subgraph of G obtained by deleting (ie removing) vi from G.

Deletion of a vertex always implies the deletion of all edges on that graph.

$vertexDelSubgraph$

Edge deleted subgraph

If ej is an edge in G, then G-ej is a subgrpah of Gobtained by deleting ej from G. Deletion of an edge does not imply deletion of its end vertices. Therefore G-ej = G(xor)ej